Probability and Statistics symbols and signs

Details: Category: Mathematics notes and reviews

Probability and statistics symbols

Symbol	Symbol Name	Meaning / definition	Example
P(A)	probability function	probability of event A	P(A) = 0.5
P(A ⋂ B)	probability of events intersection	probability that of events A and B	P(A⋂B) = 0.5
P(A ⋃ B)	probability of events union	probability that of events A or B	P(A⋃B) = 0.5
P(A \| B)	conditional probability function	probability of event A given event B occured	P(A \| B) = 0.3
f (x)	probability density function (pdf)	P(a ≤ x ≤ b) = ∫ f (x) dx
F(x)	cumulative distribution function (cdf)	F(x) = P(X≤ x)
μ	population mean	mean of population values	μ = 10
E(X)	expectation value	expected value of random variable X	E(X) = 10
E(X \| Y)	conditional expectation	expected value of random variable X given Y	E(X \| Y=2) = 5
var(X)	variance	variance of random variable X	var(X) = 4
σ²	variance	variance of population values	σ²= 4
std(X)	standard deviation	standard deviation of random variable X	std(X) = 2
σ_X	standard deviation	standard deviation value of random variable X	σ_X= 2
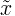	median	middle value of random variable x
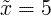cov(X,Y)	covariance	covariance of random variables X and Y	cov(X,Y) = 4
corr(X,Y)	correlation	correlation of random variables X and Y	corr(X,Y) = 0.6
ρ_X,Y	correlation	correlation of random variables X and Y	ρ_X,Y = 0.6
∑	summation	summation - sum of all values in range of series
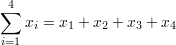∑∑	double summation	double summation
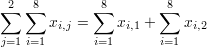Mo	mode	value that occurs most frequently in population
MR	mid-range	MR = (x_max+x_min)/2
Md	sample median	half the population is below this value
Q₁	lower / first quartile	25% of population are below this value
Q₂	median / second quartile	50% of population are below this value = median of samples
Q₃	upper / third quartile	75% of population are below this value
x	sample mean	average / arithmetic mean	x = (2+5+9) / 3 = 5.333
s²	sample variance	population samples variance estimator	s² = 4
s	sample standard deviation	population samples standard deviation estimator	s = 2
z_x	standard score	z_x = (x-x) / s_x
X ~	distribution of X	distribution of random variable X	X ~ N(0,3)
N(μ,σ²)	normal distribution	gaussian distribution	X ~ N(0,3)
U(a,b)	uniform distribution	equal probability in range a,b	X ~ U(0,3)
exp(λ)	exponential distribution	f (x) = λe^-λx , x≥0
gamma(c, λ)	gamma distribution	f (x) = λ c x^c-1e^-λx / Γ(c), x≥0
χ²(k)	chi-square distribution	f (x) = x^k^/2-1e^-x/2 / ( 2^k/2Γ(k/2) )
F (k₁, k₂)	F distribution
Bin(n,p)	binomial distribution	f (k) = _nC_k p^k(1-p)^n-k
Poisson(λ)	Poisson distribution	f (k) = λ^ke^-λ / k!
Geom(p)	geometric distribution	f (k) = p(1-p)^k
HG(N,K,n)	hyper-geometric distribution
Bern(p)	Bernoulli distribution